Un ejemplo. Circunferencia circunscrita a un triángulo

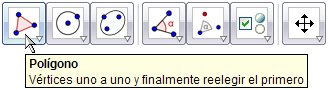
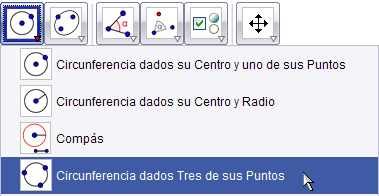
El objetivo es construir un triángulo cualquiera ("modificable con el ratón") y a partir de él la circunferencia que lo circunscribe. También deseamos conocer el centro de esa circunferencia.

Lo haremos de una forma distinta a la que suele ser habitual. Normalmente, encontraríamos el circuncentro como intersección de dos mediatrices. Si lo que deseamos es precisamente enseñar el lugar geométrico que equidista de dos puntos, no hay duda de que ese debe ser el procedimiento. Pero si lo que queremos es simplemente construir la circunferencia circunscrita y su centro lo más rápido y fácilmente posible, hay otras opciones.

Etapa 1 Seleccionar Polígono. Clic en tres posiciones distintas (A, B y C) de la Vista Gráfica. Para acabar la construcción del triángulo hace falta "cerrarlo" volviendo a hacer clic sobre el primero de los vértices (A).

Ya hemos construido un triángulo "cualquiera". Comprobemos que podemos mover sus vértices a voluntad, arrastrándolos con el ratón con   Elige-y-Mueve.

Etapa 2 Seleccionar  Circunferencia-3-puntos, que se hace visible al desplegar la lista de botones pulsando sobre la flechita de la esquina inferior derecha del botón visible  Circunferencia. Clic en los tres vértices (A, B y C) del triángulo.

Comprobemos ahora que al mover los vértices del triángulo, que son objetos "libres", se desencadena la reacomodación automática del objeto "dependiente" (la circunferencia), pues se encuentra forzada a mantener la relación que la vincula a los vértices.

 No obstante, también podemos desplazar toda la circunferencia (clic y arrastre), llevándonos con ella los puntos y el triángulo. Pero en este último caso lo único que conseguimos es situar la construcción en otra región del plano, simplemente, sin variar en nada las propiedades intrínsecas de los objetos geométricos implicados, al contrario de lo que pasa al mover un punto libre.

Por último, para localizar el centro de la circunferencia -el circuncentro del triángulo- debemos buscar un punto que esté en la mediatriz de A y B (pues ahí están todos los que equidistan de A y B) y que también esté en la mediatriz de B y C (pues ahí están todos los que equidistan de B y C). Evidentemente, el punto lo encontraremos en la intersección de ambas mediatrices. Observemos que las mediatrices pueden entenderse como "mediatrices de los lados" del triángulo o como "mediatrices de las cuerdas" de la circunferencia, pues los segmentos son los mismos.

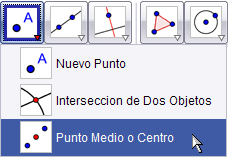
Sin embargo, supondremos estos conceptos matemáticos ya conocidos y optaremos por la vía más rápida. Simplemente pediremos a GeoGebra que nos indique el centro de la circunferencia creada.

Etapa 3 Seleccionar  Centro. Clic sobre la circunferencia.  Justo después, sin pulsar nada más, escribir con el teclado la letra O. Surgirá un cuadro emergente con la letra O escrita en el campo de introducción de texto. Pulsar OK.

En el último paso hemos aprovechado que acabamos de crear el circuncentro para inmediatamente renombrarlo con la letra O (le hubiera correspondido la letra D). También podríamos renombrarlo en otro momento, escogiendo de nuevo  Elige-y-Mueve, haciendo clic sobre el punto con esa herramienta para "marcarlo" y escribir O.