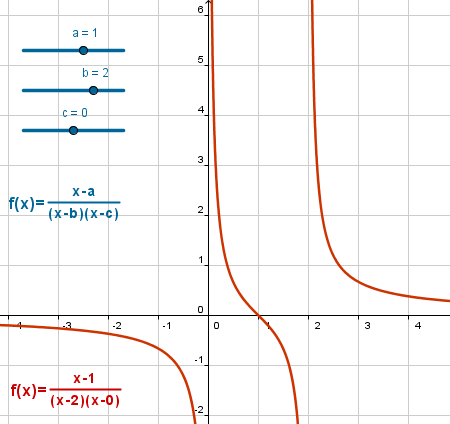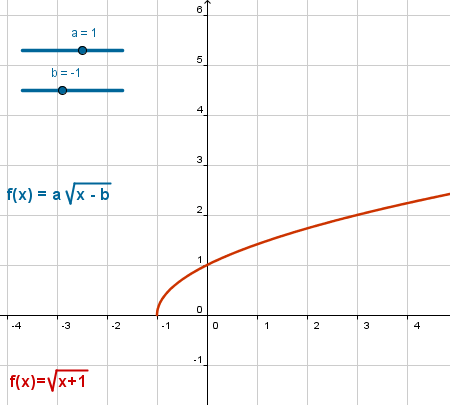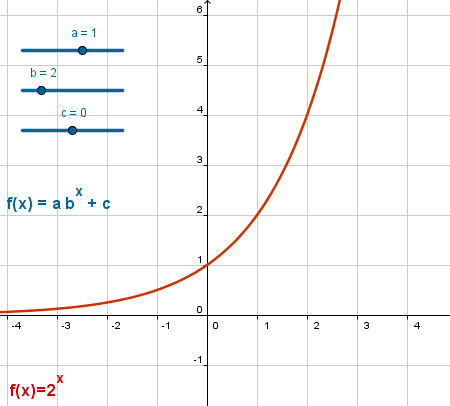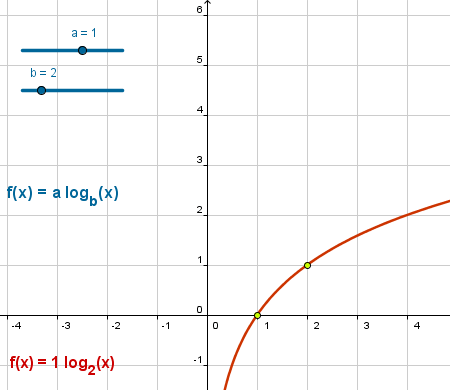|
|
► 2. Construcciones ultraligeras
► 2.+ Otros modelos
Otros ejemplos para observar y analizar
|
Con una imagen adecuada de fondo, en muy poco tiempo podemos diseñar una construcción atractiva.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
Si deseamos una imagen de alta calidad usando la propiedad Color Dinámico, en vez de "barrer" la pantalla manualmente, podemos crear varios puntos de tamaño mínimo que realicen el barrido de forma automática.
En la siguiente imagen se puede ver el resultado de uno de esos barridos. En este caso, corresponde a la condición:
donde dA y dB son las distancias de cada punto que va barriendo a dos puntos fijos A y B.
Todos las posiciones para las cuales dA - dB^0.5, en valor absoluto, obtengan el mismo valor tendrán igual color.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
En la siguiente construcción podemos generar un "mapa" de los puntos cuya suma de distancias a una circunferencia y a un punto fijos es constante (el punto fijo está en naranja, la circunferencia fija es "el sol" central).
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
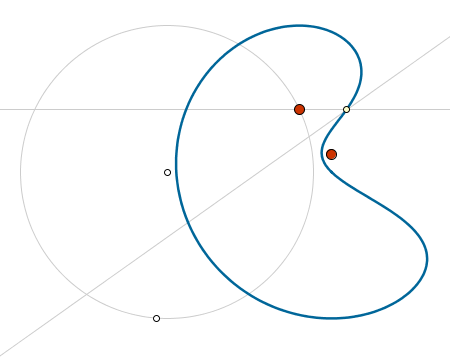
Con GeoGebra explorar nuevos lugares geométricos es sólo cuestión de imaginación. En la siguiente construcción podemos explorar las distintas formas que adquiere el lugar geométrico de los puntos que distan lo mismo de un punto fijo que de otro que se desplaza sobre una circunferencia y se mantienen a la misma altura que éste. ¿Qué sucede cuando el punto fijo se sitúa sobre la circunferencia?
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
La edición de textos con LaTeX nos permite editar fórmulas y ecuaciones. En la sección LaTeX de la ayuda se muestran los detalles.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
En este ejemplo se incluye el tratamiento de los puntos con discontinuidad evitable y los tres tipos de asíntotas (horizontal, oblicua y vertical).
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
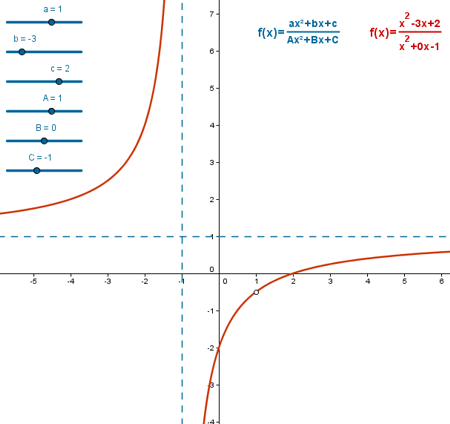
El objetivo principal ya no es representar gráficamente una función sino analizar sus propiedades locales y globales (en sí misma o en el contexto de un enunciado) con ayuda de las dos expresiones: gráfica y analítica.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
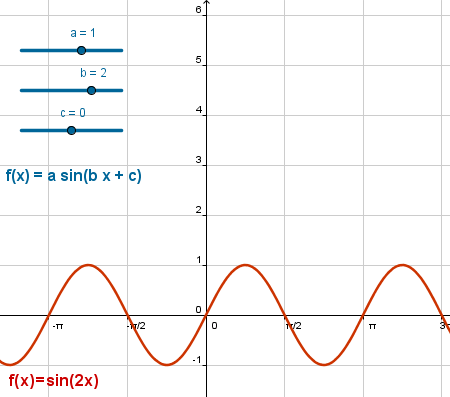
Las propiedades comunes a una familia de funciones son mucho más fáciles de observar con ayuda de gráficas interactivas.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
En el apartado "Otros modelos" del módulo 3, el modelo Logarítmico muestra plantillas de papel logarítmico y semilogarítmico.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
En las propiedades de la Vista Gráfica podemos elegir graduar los ejes
con múltiplos del número
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
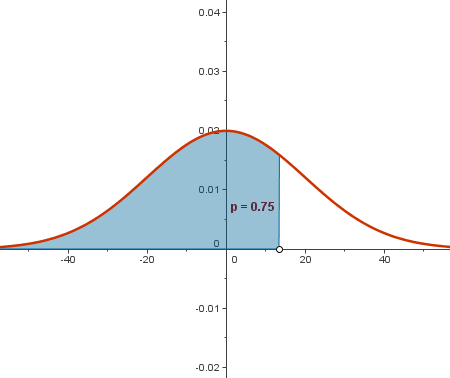
El comando Integral nos permite visualizar áreas por debajo de las curvas.
|
|
Clic en esta imagen abre la construcción de GeoGebra
|