Objetivos

Podemos mantener en todo instante un control absoluto sobre la posición de todos los objetos incluso cuando recorren itinerarios combinados.

En esta actividad mostraremos dos ejemplos. En el primero, con sólo dos puntos y cinco "estaciones". En el segundo, se trata de usar un deslizador para mostrar una disección del trapecio con el objetivo de transformarlo en un rectángulo de igual área.

Herramientas y comandos

Usaremos los comandos  Máximo, Mínimo, Polígono, PuntoMedio, RazónSimple, Rota y Si así como las herramientas:

	Punto		Intersección		Centro
	Recta		Segmento		Semirrecta
	Perpendicular		Paralela		Texto
	Deslizador

 Los objetos creados por las herramientas con fondo verde son desplazables (a no ser que su definición se base en puntos que no sean libres).

Construcción (previa) paso a paso

Preparación No No Automático

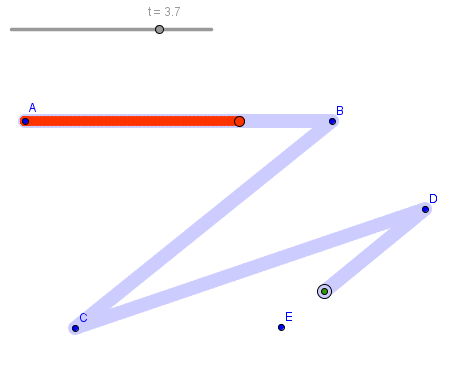
Veamos el ejemplo de introducción.

Etapa 1 Creamos un  Deslizador entre 0 y 5, con incremento 0.01. Lo renombramos como "t" y le asignamos el valor 0. Con la herramienta  Punto, creamos 5 puntos (A, B, C, D y E) en diversas posiciones. Entrada (es aconsejable usar copiar-pegar): P = Si[t < 1, t B + (1 - t) A, Si[t < 2, (t - 1) C + (2 - t) B, Si[t < 3, (t - 2) D + (3 - t) C, Si[t < 4, (t - 3) E + (4 - t) D, (t - 4) A + (5 - t) E]]]]   Q = Si[t < 3, A, Si[ t < 4, (t - 3) B + (4 - t) A, B]]

Observemos que para mover el punto P entre A y B, cuando t varía entre 0 y 1, definimos P = t B + (1 - t) A. El resto de las definiciones que aparecen en el condicional, a tramos, es similar.

Una elegante alternativa al condicional tan largo consiste definir previamente una función auxiliar:

z(x) = Si[x < 0, 0, Si[x > 1, 1, x]]

Con lo que P y Q se pueden definir abreviadamente como:

P = A + z(t) (B-A) + z(t-1) (C-B) + z(t-2) (D-C) + z(t-3) (E-D) + z(t-4) (A-E)

Q = A + z(t-3) (B-A)

Ejemplo de construcción

Encadenado

Clic en esta imagen abre la construcción de GeoGebra

Construcción paso a paso

 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

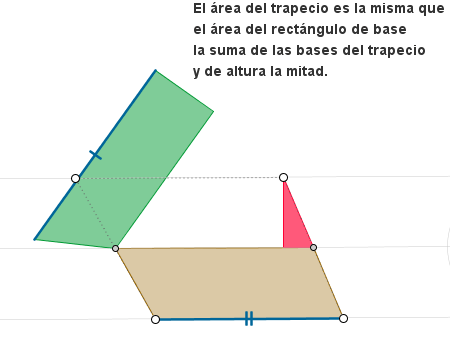
Realizaremos ahora la construcción del área del trapecio, en una nueva construcción.

Etapa 2 Creamos un  Deslizador entre 0 y 3, con incremento 0.01. Lo renombramos como "t" y le asignamos el valor 0. Herramienta  Punto. Creamos 3 puntos (A, B, C) en diversas posiciones; serán tres de los vértices del trapecio de base AB. Herramienta  Recta. Creamos la recta (a) que pasa por A y B, y la recta (b) que pasa por B y C. Herramienta  Paralela. Creamos la recta (c) paralela a la recta "a" por el punto C y la paralela (d) a la recta "b" por A. Herramienta  Intersección. Punto (D) de intersección de las dos rectas anteriores (c y d). Herramienta  Semirrecta. Semirrecta que pasa por C y D. Herramienta  Punto. Creamos un punto (E) en la semirrecta anterior; será el cuarto vértice del trapecio.  Con el uso de la semirrecta, forzamos al polígono a ser simple, impidiendo la aparición de un "trapecio cruzado". Herramienta  Segmento. Creamos los lados del trapecio: AB (f), BC, CE y EA.

Ahora diseccionaremos el trapecio trazando una altura. Deseamos que la altura se encuentre en el interior del trapecio, para proceder a la disección. Tendremos que distinguir dos casos.

Etapa 3 Herramienta  Perpendicular. Creamos la recta (j) perpendicular a la recta "a" por el punto C. Herramienta  Intersección. Punto (F) de intersección de la perpendicular anterior con la recta "a". Creamos el valor booleano para la condición del caso 1: Entrada: caso1 = RazónSimple[A,B,F] < 1

Creamos la base de la animación.

Etapa 4 Herramienta Centro. Indicamos los puntos medios de AE (G) y BC (H). Entrada: I = Si[RazónSimple[G, H, PuntoMedio[C, F]] < 0, G, PuntoMedio[C, F]] Entrada: Si[caso1, Polígono[A, B, H, G]] Creamos el ángulo de rotación . Entrada: Mínimo[t, 1] 180° Creamos el ángulo de rotación β. Entrada: Máximo[t, 2] 180° Entrada: Si[caso1, Rota[Polígono[C, I, H], -β, H]] Si[caso1, Rota[Polígono[E, C, I, G], α, G]]

Si lo deseamos, podemos repetir el proceso seguido en las dos últimas etapas para contemplar el caso 2 (cuando F no esté definido porque la altura cae fuera del lado).

Ultimamos la construcción añadiendo un texto.

Etapa 5 Herramienta  Texto. Añadimos un texto descriptivo: "El área del trapecio es la misma que el área del rectángulo de base la suma de las bases del trapecio y de altura la mitad."

Ejemplo de construcción

Trapecio

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que transforme un rombo cualquiera en un rectángulo. Sugerencia: es posible que, en este caso, sea más sencillo usar traslaciones en vez de rotaciones.

Comentarios

La combinación de varios movimientos es semejante a la integración de las distintas partes de una demostración. Habitualmente, cada parte es regida por una idea (en nuestro caso, una transformación, un movimiento plano). Esto permite reconocer mucho mejor la esencia de la demostración como una "serie dirigida de pasos" hacia el objetivo final (la tesis).

Por otra parte, la posibilidad de encadenar movimientos enriquece enormemente las posibilidades visuales. Varios objetos pueden estar moviéndose a la vez, todos ellos controlados por el mismo parámetro (o expresiones dependientes de ese parámetro).

 Investigación:

• ¿De qué forma se puede convertir un rectángulo en un cuadrado de igual área? ¿Cómo se puede realizar la "cuadratura" de un triángulo equilátero? ¿Existen cuadraturas para otros polígonos regulares? ¿Todos los polígonos regulares son "cuadrables" (mediante disecciones)?