PDF                Anterior    Siguiente

► 8. Subconstrucciones

       ► 8.3 Azulejos

Objetivos

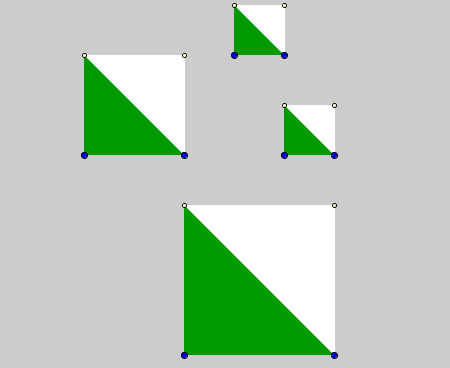
Un simple azulejo cuadrado, pintado de forma que queden distinguidos dos triángulos congruentes, puede dar mucho juego, siempre que dispongamos de varios azulejos idénticos: frisos, mosaicos, figuras...

Aunque en la mano todos los azulejos sean iguales, a la hora de colocarlos debemos decidir la orientación. En este caso, tenemos 4 modos diferentes de colocar el azulejo. Podemos crearlos diferenciados, o bien crear sólo uno y girarlo con la herramienta Rota (debajo de la herramienta fundamental Elige-y-Mueve) cuando sea necesario.

Herramientas y comandos

Usaremos el comando Polígono y la herramienta:

Polígono-regular

También veremos el uso de las listas para evitar la creación de objetos innecesarios.

Construcción paso a paso

Primero guardamos en un lugar localizable del disco duro la imagen que asignaremos a la nueva herramienta.

Práctica Preparación

No

No

Automático

  • Guardar la imagen, que servirá de icono de la herramienta que vamos a crear, en el disco duro (hacer clic derecho sobre la imagen y elegir "Guardar imagen como..."):
 
Baldosa 1 2 3 4

En nuestro caso, usaremos la baldosa 1.

Creamos el patrón.

Práctica Etapa 1
  • Herramienta Polígono-regular. Creamos el cuadrado de lado AB (los puntos A y B se crean al hacer clic con la herramienta).
  • Entrada:

{Polígono[A,B,D]}

{Polígono[B,D,C]}

C' = C

D' = D

Sombreamos las listas con el color deseado y aplicamos el estilo que queramos a los puntos C' y D'.

 Al introducir los polígonos como listas evitamos la creación redundante de vértices y lados, sólo añadimos el sombreado. Los puntos C' y D' nos permiten conservar el estilo (color, tamaño) como objetos de salida (C y D son generados al crear el polígono regular).

Ahora crearemos la nueva herramienta.

Práctica Etapa 2
  • En el menú Herramientas, pulsamos sobre "Creación de Herramienta Nueva".
  • En la primera pestaña, "Objetos de Salida", elegimos mediante la lista desplegable los objetos lista1, lista2, C' y D'.
  • En la segunda pestaña, "Objetos de Entrada", elegimos los puntos A y B (detectados automáticamente por GeoGebra).

  • En la última pestaña, "Nombre e icono", como nombre de herramienta escribimos:

    Baldosa 1

    como ayuda a la herramienta escribimos:

    Dos puntos

    y como icono buscamos y seleccionamos la imagen que hemos guardado previamente.

  • Pulsamos el botón Concluido.

Podemos probar la nueva herramienta haciendo un par de clics en la Vista Gráfica (o pulsando sobre dos puntos ya existentes).

Guardaremos la nueva herramienta como un archivo GGT, para poder usarla en cualquier construcción:

Práctica Etapa 3
  • En el menú Herramientas, pulsamos sobre "Gestión de Herramientas".
  • Elegimos la herramienta Baldosa1 (si es que hay alguna más) y pulsamos sobre el botón "Guardar como..."
  • Elegimos un lugar fácilmente localizable del disco duro y guardamos allí la nueva herramienta con el nombre "baldosa1" (el archivo se llamará "baldosa1.ggt")

Guardamos el archivo con el nombre de baldosa1.ggb.

Ahora probaremos a abrir la herramienta "baldosa1.ggt" desde cualquier otra construcción.

Ejemplo de construcción
Práctica Baldosa 1

 

 

Construcción: Azulejo 1

Clic en esta imagen abre la construcción de GeoGebra

 
Práctica Azulejos

 

 

Construcción: Azulejos

Clic en esta imagen abre la construcción de GeoGebra

 
Práctica Propuesta de construcción

 

 

Realizar la construcción de la herramienta personal correspondiente al azulejo 2.

 
Comentarios

El trabajo con figuras que hacen de patrón tiene varias vertientes:

  • Podemos analizar la propia figura (proporciones de longitudes y áreas, ángulos, simetrías, regularidad...).
  • Podemos buscar una clasificación exhaustiva bajo un determinado criterio. ¿De cuántas formas distintas se pueden disponer dos elementos, tres elementos...? ¿Qué se entiende por "distintas"?
  • Podemos proponer la reproducción de una figura ya construida.
  • Podemos invitar a que cada cual diseñe la configuración que más le agrade.
  • Podemos combinarlas con otras figuras, o preguntarnos qué variaciones de la figura serían necesarias para dotarla de determina propiedad.

Investigación Investigación:

  • Buscar en Internet ejemplos de frisos o cenefas y teselaciones, así como clasificaciones de las mismas.

 

Anterior    Arriba     Siguiente