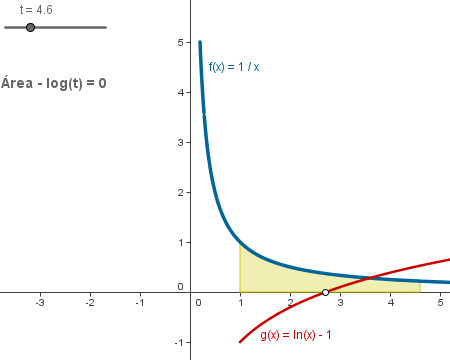|
|
► 11. Conexiones matemáticas
► 11.2 Producto
Objetivos
Queremos usar GeoGebra para proponer ejemplos de relaciones entre operaciones aritméticas y geométricas.
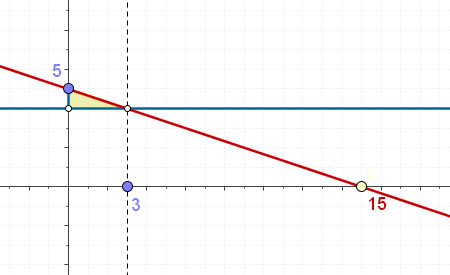
En este caso, nos basaremos en la consideración del producto a·b como raíz de la recta y = -x/a + b. Se formarán dos triángulos semejantes, en "posición de Tales". La proporcionalidad de sus lados permite hallar el producto de los dos números.
Herramientas y comandos
Usaremos el comando Polígono y las siguientes herramientas.
|
|
Punto |
|
Intersección |
|
Recta |
|
|
Segmento |
|
Perpendicular |
|
Texto |
Los objetos creados por las herramientas con fondo verde son desplazables (a no ser que su definición se base en puntos que no sean libres).
Construcción paso a paso
Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.
Preparamos el escenario.
|
Construimos la figura (la lista en la última entrada impide la creación de los segmentos y vértices del polígono, pues no los necesitamos, sólo precisamos del relleno).
|
Creamos los textos dinámicos (el operador floor impide que se visualicen decimales cuando desplazamos rápidamente los puntos).
|
Ejemplo de construcción
|
|
|
Clic en esta imagen abre la construcción de GeoGebra
|
|
|
|
Realizar una construcción similar que corresponda a la consideración del cociente b/a como raíz de la recta y = -a x + b:
|
Comentarios
Aunque la construcción está realizada para enteros, no hay problema en generalizarla para dos reales cualesquiera.
Las operaciones de suma y resta son mucho más sencillas (y habituales). Con
las cuatro operaciones podemos construir gráficamente el conjunto de los números
racionales. Algunos números irracionales, como por ejemplo todos los radicales,
también se pueden construir gráficamente de forma sencilla. Los números
trascendentes, como ![]() o
e, necesitan el auxilio de
funciones, como las trigonométricas o logarítmicas.
o
e, necesitan el auxilio de
funciones, como las trigonométricas o logarítmicas.
![]() Investigación:
Investigación:
- ¿Se puede definir la función logarítmica (natural) como función de área
L(x) bajo la curva y = 1/t en el intervalo [1, x]? ¿Se puede definir el número
e como la raíz de la curva
y = L(x)-1? ¿Cómo se podría definir, como raíz única, el número
 ?
?