Construcción paso a paso

 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página.

Primero guardamos una imagen que usaremos como icono de una herramienta personal que crearemos más adelante.

Preparación Sí No Automático Guardar la imagen que servirá de icono de la herramienta que vamos a crear en el disco duro (hacer clic derecho sobre la imagen y elegir "Guardar imagen como..."):

Creamos dos ángulos independientes, y β, que harán el papel de ángulo de inclinación y ángulo de rotación, respectivamente.

Etapa 1 Punto A (libre) Circunferencia c: Circunferencia con centro A y radio 1 Punto B: A + (3, 0) Circunferencia d: Circunferencia con centro B y radio 1 Punto C: A + (1, 0) Punto D: A + (4, 0) Punto E: Punto en c Punto F: Punto en d Ángulo : Ángulo entre C, A, E Ángulo β: Ángulo entre D, B, F

Construimos una lista (llamada puntoLista) con las tres coordenadas {p_x, p_y, p_z} de un punto cualquiera (en este caso, {4,4,4}).

Etapa 2 Lista (objeto libre): puntoLista = {4, 4, 4} Número px: p_x = Elemento[puntoLista, 1] Número py: p_y = Elemento[puntoLista, 2] Número pz: p_z = Elemento[puntoLista, 3]

Ahora realizamos la proyección al plano del punto tridimensional anterior:

Etapa 3 P444 = (p_x sin(β) + p_y cos(β), -p_x cos(β) sin(α) + p_y sin(β) sin(α) + p_z cos(α))

Convertimos esa proyección en una nueva herramienta, a través del menú Herramientas > Creación de Herramienta Nueva, guardándola con el nombre de P3D.ggt:

Etapa 4 Objeto de Salida: P444 Objetos de Entrada: , β, puntoLista Nombre de Herramienta y de Comando: P3D Icono: P3D.png (imagen de 30x30 píxeles guardada en la preparación)

Así ya podemos usar esa herramienta en cualquier construcción. La probamos (en forma de Comando, por ejemplo) creando una nueva proyección:

Etapa 5 P044 = P3D[α, β, {0,4,4}]

Al mover los ángulos y β, los puntos proyectados simulan las tres dimensiones.

Ejemplo de construcción

Proyección

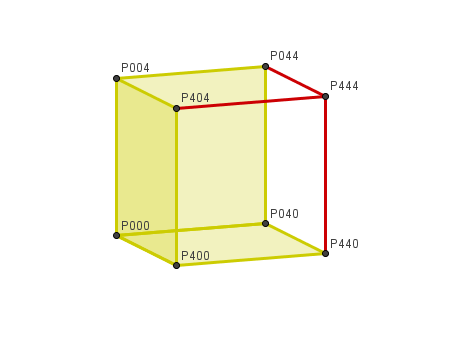
Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que permita rotar el cubo alrededor de su centro, en vez de alrededor de una arista.

Comentarios

En la construcción de ejemplo hemos creado más puntos hasta completar los vértices de un cubo y hemos completado la figura con los polígonos de algunas caras. También hemos añadido algún texto.

 Investigación:

• Al tratarse de proyecciones, los ángulos que se puedan medir en la pantalla no corresponderán, en general, con los verdaderos ángulos de entre los puntos tridimensionales. Por ejemplo, cada ángulo de cada dos aristas contiguas en cada cara del cubo es siempre constante (90º) pero varía en la proyección al rotar el cubo. La geometría analítica puede ayudarnos a crear una herramienta para medir el verdadero valor de esos ángulos. ¿Cómo?