► 13. Applets, JavaScript y XML

► 13.3 URL

Objetivos

Si navegando por Internet nos encontramos con una construcción de GeoGebra y queremos descargarla en nuestro disco duro, lo podemos hacer sin demasiados problemas, una vez que conocemos el procedimiento para hacerlo.

Lo primero que debemos intentar es abrir la construcción en una ventana independiente haciendo doble clic sobre el applet. Una vez abierta, desde el menú Archivo podemos guardar la construcción en la ubicación que deseemos.

Sin embargo, la posibilidad de abrir la construcción en una ventana independiente es una opción de configuración, un parámetro, que puede estar activado o no, a criterio de la persona que realizó la exportación de la construcción a la página web. Necesitamos, pues, otro procedimiento que también sea válido en el caso de que no se encuentre activada esa opción.

Uniform Resource Locator (URL)

Cada recurso, es decir, cualquier tipo de archivo, que se encuentre en Internet necesita una dirección para ser localizado. Esta dirección se conoce como URL. Realiza el mismo papel que una dirección postal: es necesaria para poder localizar al destinatario.

La sintaxis habitual en Internet de esas direcciones es:

http://dominio/... /... (carpetas) .../.../archivo

El nombre del protocolo (http://) es lo primero. El nombre del dominio (o servidor o anfitrión) es el que se encuentra después de la doble barra //). El resto de la dirección se llama ruta.

Por ejemplo:

http://geogebra.es/cvg/13/index.html

es la dirección de la página web index.html situada en Internet (protocolo http://), en el dominio "geogebra.es" y con ruta "/cvg/13/index.html".

A su vez, las páginas web usan las URL para integrar los diferentes elementos a los que llaman (imágenes, sonidos, animaciones, etc.).

Por ejemplo:

http://geogebra.es/cvg/ggb/pi.ggb

es la dirección de un archivo (una construcción de GeoGebra, en este caso) llamado "pi.ggb".

Las anteriores son direcciones absolutas. Pero también existe otra posibilidad, las denominadas direcciones relativas.

Si estoy en un barrio de una ciudad y pregunto a un vecino por la dirección de Urola, la tienda de animales, puede responderme con el nombre de la calle y el número (dirección absoluta) o simplemente con "en esta misma calle, más adelante, a la derecha" (dirección relativa).

Las direcciones relativas toman como referencia la dirección absoluta del recurso en donde aparece tal dirección relativa (de la misma forma que el vecino toma como referencia la calle en donde se encuentra él mismo en ese instante).

Veamos varios ejemplos de sintaxis de direcciones relativas. Supongamos antes de nada que tenemos una página web alojada en la dirección absoluta:

http://geogebra.es/cvg/html/pi.html

Así que la referencia a tener en cuenta, para saber dónde está la página pi.html, es "http://geogebra.es/cvg/html/".

En tal caso:

Dir. relativa	Dir. absoluta	Descripción
pi.ggb	http://geogebra.es/cvg/html/pi.ggb	La ruta para llegar al archivo buscado es la misma que para llegar a la página web que lo llama.
geo/pi.ggb	http://geogebra.es/cvg/html/geo/pi.ggb	El archivo buscado se encuentra en la subcarpeta "geo" que a su vez se encuentra en la misma ruta de la página web.
geo/4/pi.ggb	http://geogebra.es/cvg/html/geo/4/pi.ggb	El archivo buscado se encuentra en la subcarpeta "4" de la subcarpeta "geo" que a su vez se encuentra en la misma ruta de la página web.
../pi.ggb	http://geogebra.es/cvg/pi.ggb	El archivo buscado se encuentra en la carpeta "anterior" (llamada "padre", situada a un nivel superior) en la ruta de la página web.
../../pi.ggb	http://geogebra.es/pi.ggb	El archivo buscado se encuentra en la carpeta "anterior a la anterior" (situada a dos niveles por encima) en la ruta de la página web.
/pi.ggb	http://geogebra.es/pi.ggb	El archivo buscado se encuentra en la carpeta "raíz" del dominio, en el nivel más alto de la ruta.

Descarga de una construcción de GeoGebra

Supongamos ahora que estamos navegando por Internet y encontramos una construcción de GeoGebra (o cualquier otro applet de Java) y queremos descargarlo. El doble clic no está activado.

Lo primero que tenemos que hacer es ver el código fuente de la página. Buscamos esa opción en el navegador (menú Ver; para esta tarea recomendamos el navegador Mozilla Firefox, que dispone de un buen visor en color). Una vez que el navegador nos muestra el código de la página en el editor de texto, usamos la herramienta Buscar de ese editor para localizar las expresiones <applet. El valor asignado a la propiedad codebase y al parámetro filename nos permitirá averiguar la dirección absoluta en la que se encuentra la construcción de GeoGebra y descargarla.

Ejemplo de descarga

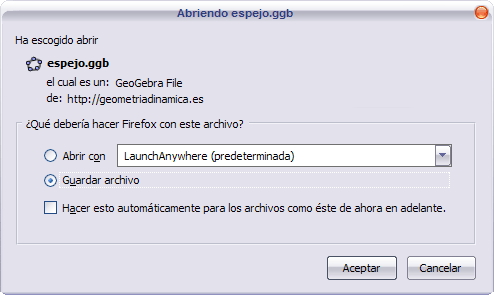
Queremos descargar la construcción que se encuentra en la página web:

http://geometriadinamica.es/Geometria/Semejanza-y-Tales/Mirandote-en-el-espejo.html

Etapa 1

Al hacer doble clic vemos que no nos deja abrir la construcción en una ventana independiente. En el menú Ver del navegador elegimos ver el código fuente de la página. Una vez mostrado, en el menú Editar del editor elegimos Buscar y escribimos:

<applet

El visor del editor se desplazará para mostrar el texto encontrado:

<applet height="520" width="750" code="geogebra.GeoGebraApplet" archive="...

Recorremos el código desde <applet hasta encontrar codebase:

codebase="/applets/losada/01"

Copiamos su valor al portapapeles:

/applets/losada/01

No cerramos el editor de texto todavía.

Etapa 2

Ahora tenemos que realizar el ejercicio de interpretación de esa dirección relativa. Observamos que no comienza con dos puntos, sino con barra. Eso significa que estamos ante la ruta completa, salvo el nombre del archivo (corresponde al último ejemplo de la tabla anterior, /pi.ggb). Por lo tanto, la dirección absoluta donde se encuentra la construcción es (copiamos el codebase en la barra de direcciones del navegador):

http://geometriadinamica.es/applets/losada/01/

Observemos que hemos añadido una barra al final, 01 es una carpeta, no el archivo. Todavía nos falta el nombre del archivo.

En el editor de texto seguimos leyendo después de codebase="/applets/... hasta encontrar la palabra filename. Un poco más adelante vemos:

Ahí tenemos el nombre del archivo: espejo.ggb. Basta incorporarlo a la dirección anterior para tener la dirección absoluta completa:

http://geometriadinamica.es/applets/losada/01/espejo.ggb

Ya podemos cerrar el editor.

Etapa 3

Al completar la dirección en el navegador y pulsar Intro, aparecerá el cuadro de diálogo que nos permitirá la descarga:

Si, al descargar el archivo, el navegador sustituye la extensión "ggb" por la extensión "zip" (a veces ocurre, depende de la configuración de nuestro ordenador), antes de hacer doble clic sobre el archivo espejo.zip para abrirlo debemos renombrarlo como espejo.ggb y sólo después abrirlo.

Propuesta de descarga

Intentar descargar la construcción de GeoGebra que se encuentra en la página:

http://geometriadinamica.es/Geometria/Cuerpos/Cubo-Espejo.html

Comentarios

El disponer de diversas formas de descargar archivos de Internet no nos concede autorización para apropiarnos de su autoría. Incluso aunque no se advierta en ninguna parte del sitio web la responsabilidad que pudiera derivarse del uso ilegítimo del material descargado, por pura honradez (aunque no exista ánimo de lucro) deberemos hacer constar en cualquier tipo de publicación en donde utilicemos ese material su procedencia y, si se conoce, su autoría.

Muchas de las construcciones de GeoGebra que podemos encontrar en Internet disponen de licencia de Creative Commons del tipo ShareAlike (o en España, Creative Commons Reconocimiento-NoComercial-CompartirIgual), lo que significa que tenemos libertad para su uso, modificación y publicación, siempre que mencionemos tanto la autoría como esta misma licencia de uso.

Investigación:

Buscar en Internet qué significa Creative Commons y qué tipos de licencias de uso existen.