Operaciones con matrices

La matriz:

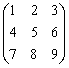
se representa en GeoGebra por filas, es decir:

M = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}.

Una matriz es una lista de listas.

Ingreso	Operación	Ejemplo
+	suma	{{1,3,5}, {2,4,6}} + {{0,2,4}, {1,3,5}}
-	resta	{{1,3,5}, {2,4,6}} - {{0,2,4}, {1,3,5}}
* o espacio	producto por escalar	3 {{1,3,5}, {2,4,6}}
	producto de matrices	{{1,3,5}, {2,4,6}}*{{1,4}, {2,5}, {3,6}}
	producto matriz 2x2 por vector (o punto)	{{1,2}, {3,4}}*(3,4) = (11,25)
	producto matriz 3x3 por vector (o punto)	{{1,2,3}, {4,5,6}, {0,0,1}}*(1,2) = (8,20)
^	potencia	{{1,2}, {3,4}}^3

 En el producto de matrices, el número de columnas de la primera matriz debe coincidir con el número de filas de la segunda. O, lo que es equivalente, cada fila de la primera matriz y cada columna de la segunda deben tener el mismo número de elementos para poder efectuar la multiplicación elemento a elemento.

 El producto de una matriz 3x3 por un vector 2x1 es posible porque GeoGebra asume que se trata de una transformación afín, donde se usan coordenadas homogéneas: (x, y, 1) para un punto y (x, y, 0) para un vector. De esta forma, el ejemplo mostrado:

{{1, 2, 3}, {4, 5, 6}, {0, 0, 1}} * (1, 2)

equivale a:

{{1, 2, 3}, {4, 5, 6}, {0, 0, 1}} * {{1}, {2}, {1}}

en el caso de que (1, 2) sea un punto, y a:

{{1, 2, 3}, {4, 5, 6}, {0, 0, 1}} * {{1}, {2}, {0}}

en el caso de que (1, 2) sea un vector.

Una vez realizado el producto de esta forma, se descarta la coordenada z resultante de este producto (que en una transformación afín es siempre 1, o indefinido, como en este último ejemplo).

 Además, existen otros comandos para realizar más operaciones con matrices:

Comando (ejemplo)	Comentario
Determinante [matriz]	Calcula el determinante de una matriz.   Ejemplo: Determinante [{{1, 2}, {3, 4}}]
MatrizInversa [matriz]	Calcula la matriz inversa de la indicada.   Ejemplo: MatrizInversa [{{1, 2}, {3, 4}}]
Traspone [matriz]	Traspone una matriz.   Ejemplo: Traspone [{{1, 2}, {3, 4}}]