Objetivos

Usar GeoGebra como geoplano.

En este ejemplo, se propondrá el cálculo del perímetro de un polígono.

Herramientas y comandos

Se necesita mostrar la cuadrícula y obligar a los puntos a permanecer en ella. Podemos elegir entre dos tipos de cuadrícula, la ortogonal y la isométrica. Finalmente, sólo necesitamos puntos que hagan de pivotes y segmentos en vez de gomas elásticas.

	Elige-y-Mueve		Punto
	Segmento		Polígono

Construcción paso a paso

Prácticamente, nos basta con preparar el escenario.

Preparación No Sí Activa (Cuadrícula)

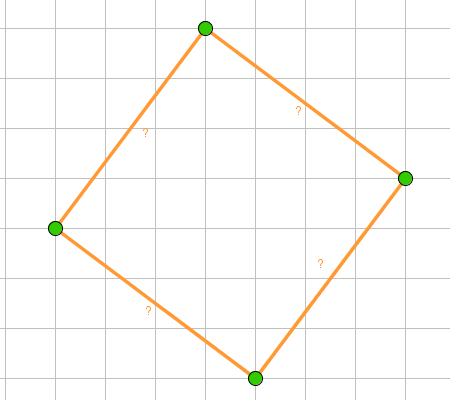
Ahora sólo nos queda colocar los puntos y segmentos (o polígonos) que deseemos y moverlos. Cualquier actividad pensada para desarrollar con un Geoplano la podemos trasladar aquí. Por ejemplo, podemos realizar actividades de cálculo perimétrico por aplicación del teorema de Pitágoras.

Construcción Herramienta  Punto. Colocar cuatro puntos sobre intersecciones de la cuadrícula. Herramienta  Segmento. Unir los cuatro puntos con segmentos haciendo clic con esta herramienta sobre cada par de puntos. [Alternativamente, se podría haber usado la herramienta Polígono para realizar este paso y el anterior a la vez, especialmente si deseamos sombrear la región cerrada con algún color.] Herramienta Elige-y-Mueve (o pulsar la tecla Esc). Probar a mover los vértices con ayuda de esta herramienta, hasta colocarlos en la posición deseada.

Ejemplo de construcción

Geoplano

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una actividad similar sobre una cuadrícula isométrica.

Comentarios

Existe una amplia documentación sobre actividades de diverso tipo para usar el recurso didáctico del geoplano en el aula. Se pueden plantear problemas de perímetros, de áreas, de ángulos, de formas, de sólo pasar por determinados puntos, la fórmula de Pick, etc. Las ventajas que aporta GeoGebra sobre el modelo físico son varias: resulta más rápido y sencillo rediseñar una construcción, las gomas elásticas (del color que se nos antoje) no se pierden ni se rompen (porque no existen), no tiene el tamaño limitado, podemos realizar cálculos directamente sobre la construcción, se pueden sombrear superficies cerradas...

 Investigación:

• El polígono del ejemplo, ¿es un cuadrado? ¿Podemos comprobar si lo es o no? ¿Cómo? ¿Existe más de una forma de comprobarlo con GeoGebra?
• En una cuadrícula ortogonal, la longitud del tercer lado del triángulo de lados 3 y 4 es 5. ¿Hay otros triángulos con sus tres lados enteros?
• En una cuadrícula isométrica, la longitud del tercer lado del triángulo de lados 3 y 5 es 7. ¿Hay otros triángulos con sus tres lados enteros?