Objetivos

Usaremos la propiedad Color Dinámico para visualizar fácilmente lugares geométricos desconocidos, siempre que sepamos expresar la condición que deben cumplir los puntos del mismo.

Este modo de empleo del color dinámico es realmente potente. Simplemente "barriendo" la pantalla el lugar geométrico aparece, como por arte de magia, ante nuestros ojos.

Herramientas y comandos

Emplearemos las siguientes herramientas:

Elige-y-Mueve

Punto

Segmento

Además, usaremos la propiedad Capa y la propiedad Color Dinámico RGB:

La propiedad Capa permite decidir qué objetos se visualizan por encima de otros, asignando a cada objeto un número entre 0 y 9. Las capas con números mayores se encuentran "encima" de las menores. Por ejemplo, un objeto visible en la capa 1 puede ocultar a un objeto visible en la capa 0, pero no al revés.

Esta propiedad Color Dinámico asigna al objeto tres valores numéricos, cada uno de ellos variable entre 0 y 1, que corresponden a la intensidad de rojo (Red), verde (Green) y azul (Blue) presentes en su color-luz combinado. Para inactivar esta propiedad se debe usar el botón X situado a la derecha del código RGB (en tal caso, el color del objeto será el establecido en la pestaña Color del cuadro de diálogo Propiedades del objeto; es la opción predefinida al crear un objeto nuevo).

En la siguiente tabla se puede apreciar (agrupados por complementarios) el resultado de la elección de algunos colores básicos.

Cuando el valor numérico "c" no esté entre 0 y 1, GeoGebra sigue la siguiente norma:

1) Si el valor numérico no está entre 0 y 2, toma su resto módulo 2.

2) Si el valor numérico "c" obtenido está entre 1 y 2, toma "2 - c".

O, si se prefiere, sigue la siguiente función: 

c(x) = 1 - abs(1 - x + 2 floor(x/2))

cuya gráfica es:

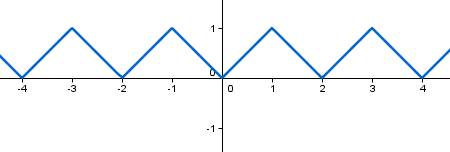
El motivo de este comportamiento es evitar cambios bruscos de color entre dos valores numéricos próximos. Obsérvese el periodo 2.

Así, si construimos un punto A y una paralela al eje Y que contenga a A (herramienta  Paralela), y le asignamos a esta recta el color dinámico (clic derecho, Propiedades) que denotaremos como RGB = [0, x(A), 0]:

entonces, al activar el rastro de la recta y moverla (mejor si desactivamos previamente la atracción de puntos a la cuadrícula, menú Opciones), obtendremos una distribución de color que sigue el patrón que muestra la siguiente imagen.

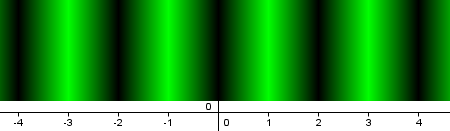
Si se quiere evitar la periodicidad, podemos optar por sustituir la expresión x(A) por la expresión e^(-abs(x(A)-1)).

La gráfica de la función y = e^(-abs(x-1)) es la siguiente:

por lo que al realizar la sustitución obtenemos una distribución de color del siguiente tipo:

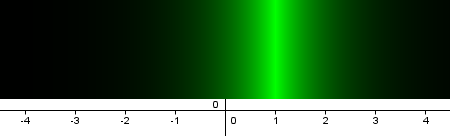
Construcción paso a paso

Tenemos dos puntos A y B. Queremos conocer el lugar geométrico de los puntos C equidistantes de ellos (la mediatriz). Para ello, establecemos como Color Dinámico del punto C la expresión a/b para cada color del RGB, donde a y b son las distancias respectivas a A y B. Al activar el Rastro y mover el punto, cuando a/b sea 1 (o entero impar), el color resultante será blanco, lo que provocará que destaque, por contraste, sobre los demás.

Preparación Sí No Desactiva

Realizaremos una construcción modelo, susceptible de adaptarse a una gran variedad de situaciones.

Etapa 1 Herramienta  Punto. Colocamos tres puntos (A, B y C). Herramienta  Segmento. Unimos A con C (a) y B con C (b). Entrada: objetivo = a/b Abrimos el cuadro de diálogo Propiedades del punto C (clic derecho), vamos a la pestaña Avanzado y asignamos ese valor numérico (objetivo) a cada uno de los tres colores base R, G, B (podemos usar Control+C y Control+V para copiar y pegar). En la pestaña Básico, activamos Mostrar Rastro. Herramienta Elige-y-Mueve (o pulsamos la tecla Esc). Probamos a mover C por toda la Vista Gráfica y observamos el resultado:

Además de la mediatriz buscada, aparecen unas circunferencias no concéntricas rodeando al punto B. Cada circunferencia reúne a los puntos C que cumplen que "a" es un múltiplo impar de "b". [Concretamente, si asignamos al punto A las coordenadas (0,0) y al punto B (1,0), la familia de circunferencias será:

(x - k)² + y² = k (k - 1)

con k = 1 + 1/(4 n (n - 1)), donde n es natural.]

Esto es debido, como hemos visto, a la periodicidad del color dinámico. Si queremos eliminar esos otros lugares geométricos, basta reasignar el objetivo:

Etapa 2 Limpiamos la pantalla tecleando Control+F (o, alternativamente, desde el ítem Actualiza Vista Gráfica del menú Vista). Entrada: objetivo = e^(-abs(a-b)) Probamos a mover C por toda la Vista Gráfica y observamos el resultado:

Cambiaremos ahora la condición objetivo. Buscamos el lugar geométrico de los puntos cuya diferencia de distancia a los puntos A(0,0) y B(1,0) vale siempre 1/2. Además, duplicaremos el punto C para evitar "perderlo" al confundirse con el fondo.

Etapa 3 Limpiamos la pantalla tecleando Control+F (o, alternativamente, desde el ítem Actualiza Vista Gráfica del menú Vista). Entrada: A = (0,0) Entrada: B = (1,0) Entrada: objetivo = abs(a-b)/0.5 Entrada: D = C Asignamos a D el tamaño 7 (clic derecho, Propiedades, Estilo) y color naranja (pestaña Color). Asignamos a C la capa 1 (clic derecho, Propiedades, Avanzado). Probamos a mover C por toda la Vista Gráfica y observamos el resultado.

Ejemplo de construcción

Fantasmas

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que muestre una o más elipses.

Comentarios

El color dinámico nos conduce rápidamente hacia el descubrimiento del lugar geométrico buscado. El tono gris claro nos indica la posible cercanía del blanco, nuestro objetivo, algo así como en el juego del "frío o caliente". Donde el punto deje un rastro oscuro nos indica "frío" (lejos del objetivo). De esta forma, las distintas luminosidades nos van facilitando cada vez más información sobre dónde se encontrará el lugar buscado.

Si preferimos obtener una imagen en color en vez de tonos de gris, podemos lograrlo simplemente variando la expresión que vale 1 cuando se alcanza la condición en cada uno de los colores RGB. Por ejemplo, el color que podemos ver en la viñeta de la izquierda (con la mediatriz fantasma; si se hace clic sobre ella se abrirá la construcción) corresponde a RGB = [e^(a-b), e^(b-a), e^(a/b-1)]. Obsérvese que cuando "a" sea igual a "b" el valor numérico RGB continuará siendo [1, 1, 1], es decir, blanco.

 Investigación:

• Las condiciones que hemos presentado como objetivo en los ejemplos anteriores son muy sencillas pero podrían ser mucho más sofisticadas. Por ejemplo, tomemos A(0,0), B(1,0), C un triángulo de base unidad. Prolonguemos sus lados. Si trazamos las bisectrices a AB y AC, cortarán al lado BC (o su prolongación) en dos puntos M y N. ¿Cuándo AM tendrá la misma longitud que AN? En este enlace se puede ver la construcción ya realizada. [Este lugar geométrico corresponde, en coordenadas polares, a la ecuación:

 r = (sin(c+)+sin(c))/(sin(c-)+sin(c))

donde c = /4.]