Objetivos

El estudio de las familias de funciones es especialmente sencillo con GeoGebra. Basta crear los deslizadores correspondientes a los coeficientes o parámetros que deseamos variar para observar su efecto en la función.

GeoGebra también permite toda clase de operaciones con funciones, incluidas la composición, derivación e integración.

En este ejemplo prepararemos una construcción que facilite la observación del papel que juega cada coeficiente de una cuadrática.

Herramientas y comandos

Veremos la diferencia entre introducir un lugar geométrico e introducir una función. También usaremos las herramientas:

Elige-y-Mueve

Texto

Construcción paso a paso

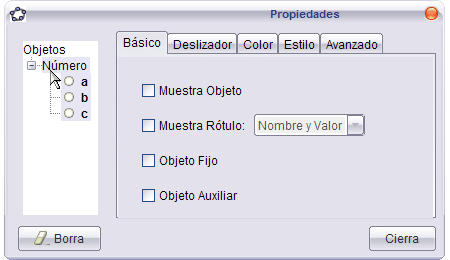
Preparamos el escenario.

Preparación Sí Sí Automático

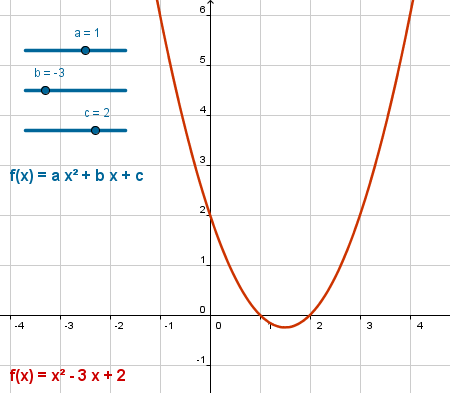
Crearemos la familia de funciones lineales.

Etapa 1 Entrada: 1  (se creará el número a). Entrada: 1  (se creará el número b). Entrada: 1  (se creará el número c). En el cuadro de diálogo Propiedades de Objeto (clic derecho sobre c por ejemplo, o clic en Propiedades del menú Edita), seleccionamos el tipo Número, que es equivalente a seleccionar todos los números, y activamos Muestra Objeto en la pestaña Básico. En el apartado Propiedades del módulo 1 se explica con detalle el uso de este cuadro de diálogo.   Este procedimiento es igual de rápido que el uso de la herramienta Deslizador, pero ofrece la ventaja de disponer los deslizadores perfectamente alineados. Posteriormente, si así lo deseamos, podríamos desplazarlos en bloque seleccionándolos a la vez con ayuda de la tecla Control o enmarcándolos con la herramienta fundamental Elige-y-Mueve. Entrada: a x^2 + b x + c  (se creará la función f).

En la expresión anterior, no hay que omitir el espacio entre "a" y "x", y entre "b" y "x", pues tal espacio es el operador de multiplicación (equivale a *). Si se omite, GeoGebra consideraría "ax" y"bx" como variables no definidas. Por otra parte, si en vez de los parámetros a, b y c colocamos números concretos (p.e., 3x^2+5x+2) podríamos omitir el operador multiplicación, pues GeoGebra sólo puede interpretar "3x" como un producto, nunca como el nombre de un objeto (los nombres siempre comienzan con una letra).

Si hubiéramos introducido la expresión y = a x^2 + b x + c (como una ecuación en x e y), GeoGebra consideraría a la cuadrática como objeto "parábola" (o "cónica") en vez de como objeto "función". La diferencia entre ambas consideraciones se revela en las distintas acciones que podemos efectuar a través de los comandos:

Comandos de parábola y = a x2 + b x + c	Comandos de función cuadrática f(x) = a x2 + b x + c
Vértice	Extremo
Tangente	Tangente
Foco	Raíz
Directriz	Factoriza
Parámetro	PolinomioTaylor
Ejes	PuntoInflexión
EjePrincipal	Simplifica
EjeSecundario	Desarrolla
Angulo	Longitud
Diámetro	Curvatura
Polar	VectorCurvatura
	CírculoOsculador
	Derivada
	Iteración
	ListaDeIteración
	SumaInferior
	SumaSuperior
	SumaTrapezoidal
	Integral

Etapa 2 Herramienta  Texto. Hacemos clic en un lugar vacío de la Vista Gráfica y editamos el texto "f(x) = " + f  También podríamos haber optado por mostrar simplemente el rótulo de f, eligiendo la opción "nombre y valor". Hay dos inconvenientes si usamos este método: no tendremos acceso a estilos de letra y no podremos posicionar con precisión el texto. Además, la posición del texto se moverá con la gráfica, lo que a veces será deseable y a veces no. Herramienta Elige-y-Mueve. Variamos los parámetros a, b y c observando en cada caso cómo afectan sus cambios a la gráfica de la función, particularmente el signo de cada uno.

Ejemplo de construcción

Funciones

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar para estudiar la familia de funciones f(x) = c / (a x + b).

Comentarios

Algo similar ocurre con la recta (como lugar geométrico) y la función afín. Si introducimos "y = 2x +3", GeoGebra entiende una recta mientras que si introducimos simplemente "2x + 3" se entenderá y nombrará como una función.

 Investigación:

• ¿Qué trayectoria describe el vértice de la parábola al variar b? Crear el vértice Extremo[f], activar su Rastro y desplazar b. Comprobar que la trayectoria del vértice sigue la función h(x)= -a x² + c. ¿Por qué?
• ¿Qué sucede con las funciones afines definidas como f(x) = a x + a? ¿Y con las cuadráticas definidas como f(x) = a x² + a x + a? Probar a activar el rastro de cada una de estas funciones antes de mover el deslizador "a".
• ¿Cómo es la familia de funciones f(x) = (25 - x^2 )^(1/n)? (n natural). ¿Convergen hacia alguna función concreta al crecer n?
• Realizar pruebas con los comandos específicos de funciones que aparecen en la tabla anterior. Para conocer la sintaxis de cada uno, basta introducir su nombre en el campo de Entrada y pulsar F1.