Objetivos

Usaremos GeoGebra para crear un generador de combinaciones lineales de dos vectores independientes. El efecto de estas combinaciones lineales se visualizará en un movimiento plano, concretamente en la traslación de un patrón para formar un mosaico de estrellas hexagonales.

Gracias al comando Secuencia podemos obtener en pocos minutos el mismo (o mejor) diseño gráfico que el que obtendríamos con las habituales herramientas de dibujo después de realizar muchos procesos repetitivos y tediosos.

 El objetivo del proceso puede ser muy distinto dependiendo del contexto matemático en el que nos desenvolvamos. Si este contexto es geométrico, dirigiremos la atención hacia el resultado de la aplicación de la traslación como movimiento plano. Si el contexto es algebraico, hacia la independencia de los vectores generadores y el concepto de combinación lineal.

Como es habitual, retocaremos a nuestro gusto el estilo de los objetos gráficos.

Herramientas y comandos

En esta actividad veremos un ejemplo de cómo crear una lista dependiente de dos variables usando el comando Secuencia.

La sintaxis que usaremos corresponderá a una Secuencia de Secuencia (es decir, una matriz):

Secuencia [Secuencia [e(s, t), s, s1, s2], t, t1, t2]

donde e(s, t) es una expresión -numérica o geométrica- dependiente de la variable s que varía entre s1 y s2, y de la variable t que varía entre t1 y t2. El resultado de esta secuencia es la matriz (lista de listas) de todos los valores u objetos {{e(s1, t1), ..., e(s2, t1)}, ...,{e(s1, t2), ..., e(s2, t2)}}

Además de la herramienta fundamental para mover y seleccionar ( Elige-y-Mueve), usaremos la herramienta Vector para establecer los vectores generadores de las combinaciones lineales y el comando Traslada (que también corresponde a una herramienta) para definir las traslaciones correspondientes. Recordemos que las herramientas que se encuentran con fondo verde indican que son creadores de objetos desplazables, al menos mientras no se fije alguno de sus elementos.

Vector

Polígono

Deslizador

Construcción paso a paso

 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Primero prepararemos el escenario.

Preparación Sí Sí (isométrica) Activa (Cuadrícula)

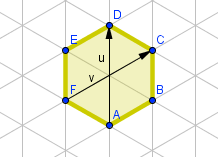
Dibujaremos un hexágono regular sobre la cuadrícula isométrica.

Etapa 1 Con ayuda de Polígono, construir un hexágono regular ABCDEF (polígono1), con dos vértices opuestos en A(0,0) y D(0,2). [Ver la imagen de la Etapa 2.] En el menú Vista, desactivar Ejes.

Ahora crearemos dos vectores independientes.

Etapa 2 Usando Vector, definir el vector (u) de A a D y el vector (v) de F a C.

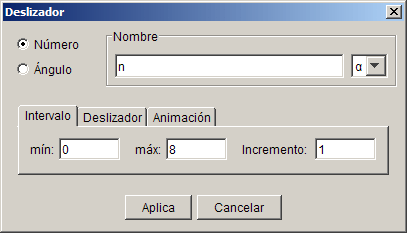
Vamos a definir un deslizador que más adelante nos servirá para establecer las cotas de los parámetros.

Etapa 3 Con ayuda de Deslizador, definir un parámetro n entre 0 y 8 con incremento de paso 1. Escoger  Elige-y-Mueve y arrastrar el segmento del deslizador hasta la posición que se desee. Fijar su posición, en el cuadro de diálogo Propiedades, para evitar su desplazamiento accidental.

Ya estamos en condiciones para crear una serie de combinaciones lineales (s u + t v) de los vectores independientes u y v que nos permitan trasladar la figura hexagonal por el plano.

Etapa 4 Entrada:          Secuencia[Secuencia[Traslada[polígono1, s u + t v], s, -n, n], t, -n, n]

Para terminar, mejoraremos el estilo.

Etapa 5 Establecer el estilo (color, grosor, sombreado...) que se considere más oportuno para los objetos creados, a través del cuadro de diálogo Propiedades.  Se debe tener en cuenta que la lista creada se comporta como un solo objeto a efectos de establecer su estilo.

Ejemplo de construcción

Estrellas

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que forme un tablero ajedrezado, un damero.

Comentarios

Una vez construida la lista de secuencias (lista1), si volvemos a mirar su definición usando el cuadro de diálogo Propiedades, veremos que GeoGebra ha modificado la definición que habíamos introducido:

Secuencia[Secuencia[Traslada[polígono1, s u + t v], s, -n, n], t, -n, n]

por esta otra:

Secuencia[Secuencia[Polígono[Traslada[A, s u + t v], Traslada[B, s u + t v], Traslada[C, s u + t v], Traslada[D, s u + t v], Traslada[E, s u + t v], Traslada[F, s u + t v]], s, -n, n], t, -n, n]

El motivo es simple: para trasladar el polígono, GeoGebra necesita trasladar los vértices que lo determinan. Evidentemente, para nosotros la primera expresión resulta mucho más breve e intuitiva que la segunda.

 Investigación:

• Probar a ejecutar el método "Secuencia de Secuencia" refiriéndose a distintos objetos. A continuación, proponemos un par de ejemplos. Pensar en algún otro tipo.

Secuencia [ Secuencia [(s, t), s, -4, 4], t, -5, 5]

Secuencia [ Secuencia [Vector[(s, t)], s, -4, 4], t, -5, 5]