Dos listas son suficientes para crear plantillas de papel logarítmico y semilogarítmico. Los objetos libres son parámetros modificables. La forma más sencilla de variar sus valores es hacer clic en el parámetro deseado y pulsar las teclas + o -.

Clic en esta imagen abre la construcción de GeoGebra

Hemos exportado la imagen como imagen vectorial (tarjetas.eps), la hemos incrustado en Word (tarjetas.doc) y también la hemos convertido a pdf (tarjetas.pdf).

Clic en esta imagen abre la construcción de GeoGebra

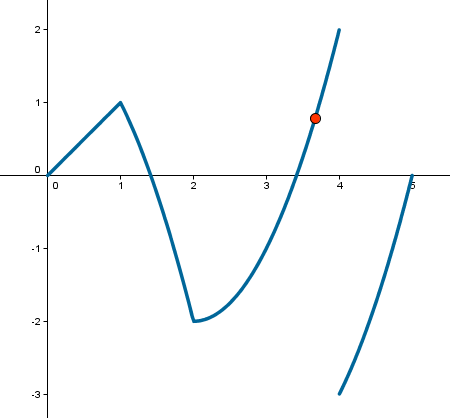
Puede usarse el comando Si para crear una función definida a trozos.

Ejemplos:

• Si [x < 1, x + 3, x - 1]
• Si [x < 1, Función[x + 4, -10, 1], x - 1]

 Pueden usarse derivadas e integrales de tales funciones e intersecarlas como funciones “normales”.

Si los trozos son muchos, el procedimiento anterior ocasiona la aparición de condicionales anidados (comandos Si dentro de otros comandos Si, etc.). En tal caso, puede ser conveniente usar una función auxiliar para ayudarnos a separar los trozos, como se muestra en el siguiente ejemplo correspondiente a una función f(x) que toma diferentes expresiones f₁(x), f₂(x), f₃(x) y f₄(x) en los intervalos [0,1), [1,2), [2,4) y [4,5], respectivamente:

z = Si[x < 0 || x ≥ 1, 0, 1]

f = Función[z(x) f_1(x) + z(x - 1) f_2(x) + z((x - 2) / 2) f_3(x) + z(x - 4) f_4(x), 0, 5]

Clic en esta imagen abre la construcción de GeoGebra

La siguiente construcción dibuja la imagen del conjunto de Mandelbrot usando la técnica del Color Dinámico (ver en el módulo 2, "Fantasmas" y "Otros modelos"). Al dibujarlo línea a línea, tarda mucho en completarlo (unas cuatro horas), pero afortunadamente es trabajo-máquina que no nos impide hacer cualquier otra cosa mientras lo ejecuta en segundo plano.

El esquema de construcción de las condiciones de color es el siguiente:

• Definimos la sucesión A, A₂ + A, ..., A_n+1 = A_n² + A

El punto A, afijo del complejo, se comporta operativamente como el propio número complejo; la potencia es la potencia compleja. El conjunto de Mandelbrot es el conjunto de los A para los cuales la sucesión de módulos de los complejos de la sucesión anterior está acotada. Colocamos un punto A y calculamos A₁, ..., A₂₀:

 

A₁ = A,    A₂ = A₁² + A,    ...A₂₀ = A₁₉² + A

 

y creamos la lista:

complejos = {A₁, A₂, A₃, .., A₁₉, A₂₀}

• Hallamos el máximo de sus módulos y asignamos un color entre 0 (negro) y 1 (blanco) a ese máximo:

color = Si[ max > 2, 1, max / 2 ]

• Damos al punto A (que trazará el dibujo) el Color Dinámico RGB:

[R, G, B] = [color, (1+color²)/2, (1+color)/2]

Clic en esta imagen abre la construcción de GeoGebra