Objetivos

Queremos aprovechar la facilidad que ofrece GeoGebra para cambiar las condiciones iniciales de muchos problemas, permitiendo de esta forma una rápida aproximación a distintos casos de los que podamos inferir una pauta o una ley.

El problema que proponemos tiene el siguiente enunciado.

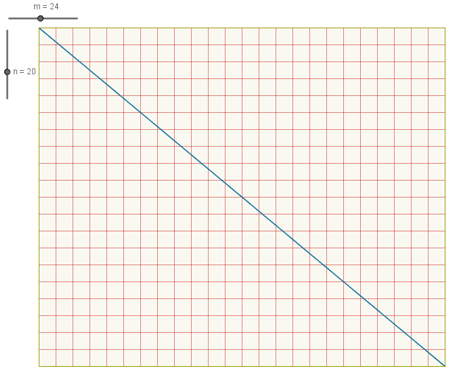
El suelo de una pequeña plaza rectangular está formado por filas de grandes losas cuadradas de idénticas dimensiones. Hay n filas, y en cada fila hay m losas. Un día, una hormiga atraviesa en línea recta la plaza, siguiendo exactamente una diagonal. ¿Cuántas losas distintas pisa la hormiga?

Dirigimos la investigación mediante las siguientes propuestas:

• Hacer m=3 y n=2. Contar y anotar la respuesta.
• Hacer m=5 y n=2. Contar y anotar la respuesta.
• Hacer m=5 y n=3. Contar y anotar la respuesta.
• Hacer m=6 y n=5. Contar y anotar la respuesta.
• Realizar una conjetura sobre la relación entre la suma de n y m, y las respuestas obtenidas.
• Hacer m=6 y n=3. Contar y anotar la respuesta. ¿Se mantiene nuestra conjetura?
• Realizar más y más experimentos, con distintos valores de m y n. Hacer dos listas: una para los valores de m y n que cumplen nuestra conjetura y otra para los que no la cumplen. Intentar encontrar en qué se diferencian esos pares de valores entre sí.
• A partir de las observaciones, realizar una nueva conjetura, hasta alcanzar una ley válida para todos los casos experimentados.

Además, aprovecharemos esta construcción para usar un método de posicionar cualquier objeto en la Vista Gráfica independientemente de la escala, así como establecer medidas que se ajusten automáticamente a las dimensiones de la Vista Gráfica.

Herramientas

Usaremos el comando Esquina para establecer una referencia basada en las dimensiones de la Vista Gráfica, no en los ejes cartesianos.

Además, usaremos los comandos Secuencia, Segmento, Máximo y Mínimo.

Construcción paso a paso

 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Preparamos el escenario.

Preparación No No Desactiva

Creamos las medidas de referencia absoluta, con respecto a la esquina superior izquierda (Esquina[4]) de la Vista Gráfica.

Etapa 1 Entrada:  m = 24 n = 20 ancho = x(Esquina[3] - Esquina[4]) alto = y(Esquina[4] - Esquina[1]) A = Esquina[4] + (ancho, -alto) / 10 inc = Mínimo[0.8 ancho / m, 0.8 alto / n]

Por último, trazamos el enlosado y el paseo.

Etapa 2 Entrada:  Secuencia[Segmento[A + (s, 0) inc, A + (s, -n) inc], s, 0, m] Secuencia[Segmento[A + (0, -s) inc, A + (m, -s) inc], s, 0, n] Segmento[A, A + (m, -n) inc]

Ejemplo de construcción

Plaza enlosada

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

Realizar una construcción similar que plantee el mismo problema salvo que ahora las losas no son cuadradas sino rectangulares, de doble largo que ancho (no es preciso resolver esta versión, sólo plantearla).

Comentarios

En la construcción de ejemplo hemos añadido un rectángulo (en forma de lista para no añadir elementos innecesarios) para mostrar un sombreado de fondo.

 Investigación:

• ¿Por qué funciona el método indicado en la etapa 1 para crear una unidad de medida ("inc") independiente del sistema de coordenadas cartesianas?