PDF                Anterior    Siguiente

► 6. Problemas dirigidos

       ► 6.4 El arco

Objetivos

Se pretende ejemplificar el uso de GeoGebra para exponer un procedimiento de construcción e invitar a su reproducción. Este sistema de aprendizaje estimula la observación a la vez que ayuda al estudiante desglosando una construcción compleja en varios pasos simples.

Herramientas

Usaremos los comandos Arco, Circunferencia, Distancia, Polígono, Recta, Refleja, Rota, Segmento y Si, junto con las siguientes herramientas.

Punto Intersección Centro
Segmento Paralela Circunferencia
Arco-centro Ángulo Refleja-en-recta
Rota-ángulo Deslizador Texto
Imagen  

Nota Los objetos creados por las herramientas con fondo verde son desplazables (a no ser que su definición se base en puntos que no sean libres).

Construcción paso a paso
 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. La propia construcción se encarga, en esta ocasión, de visualizar el proceso de construcción.

Preparamos el escenario.

Práctica Preparación

Sí

No

Desactiva

  • Guardar la siguiente imagen en el disco duro (hacer clic derecho sobre la imagen y elegir "Guardar imagen como..."):

 

En la etapa 1 introduciremos la imagen y sobre ella estableceremos los puntos de referencia.

Puede ser que el color de la imagen dificulte la visualización correcta de los objetos que vayamos creando. Por este motivo, resulta recomendable ir modificando el color o el grosor de estos objetos, a medida que los creamos, para que resalten sobre la imagen facilitando su rápida localización.

Práctica Etapa 1
  • Herramienta Deslizador. Creamos el parámetro t entre 0 y 5, con incremento de paso 0.01. Asignarle el valor 3.5.
  • Creamos una función auxiliar para simplificar el control de la animación. Entrada:

z = Si[x < 0, 0, Si[x > 1, 1, x]]

 

Ocultamos la gráfica.

  • Entrada: A = (-4, -6)
  • Herramienta Paralela. Trazamos la paralela (a) al EjeX por el punto A.
  • Herramienta Punto. Colocamos un punto en esa recta. Lo renombramos como A' y lo deslizamos hasta alcanzar la posición (5, -6) (si hace falta, activamos temporalmente la atracción de puntos a la cuadrícula).
  • Herramienta Imagen. Introducimos la imagen guardada y la posicionamos sobre los puntos anteriores (esquina 1 en A y esquina 2 en A'). Le asignamos 50% de sombreado en sus propiedades.
  • Herramienta Centro. Indicamos el punto medio entre A y A'. Lo renombramos como M.
  • Herramienta Paralela. Trazamos la paralela (b) al EjeY por el punto anterior.
  • Entrada: B = (-2.82, -1.14)  
  • Herramienta Refleja-en-recta. Reflejamos el punto B en la recta b, obteniendo el punto B'.
  • Herramienta Centro. Indicamos el punto medio entre B y B'. Lo renombramos como N.
  • Herramienta Paralela. Trazamos la paralela (c) al EjeX por el punto B.
  • Ocultamos los ejes.

Creamos un indicador del valor necesario para elevarnos hasta los centros de los arcos.

Práctica Etapa 2
  • Entrada: C = (x(M) + 5, y(B))
  • Entrada: Segmento [C, C + (0, 1)]
  • Herramienta Punto. Colocamos un punto (D) en ese segmento. Lo deslizamos hasta alcanzar la posición (5.5, -0.38) y lo fijamos.
  • Entrada: E = (x(N), y(D))
  • Herramienta Texto. Insertamos el texto "" + Distancia[D, C] debajo del punto C.

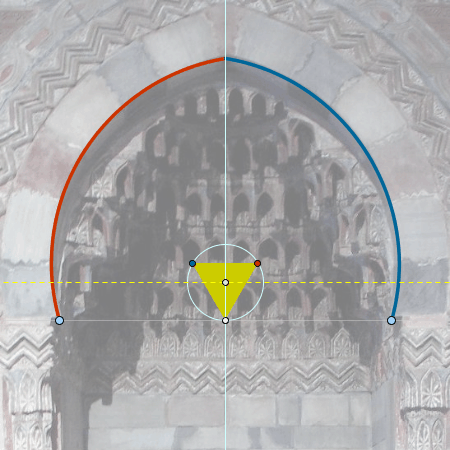
Realizamos la construcción de los arcos.

Práctica Etapa 3
  • Herramienta Circunferencia. Trazamos la circunferencia con centro E que pasa por N.
  • Herramienta Rota-ángulo. Rotamos 120º el punto N alrededor de E, obteniendo el punto N', que renombramos como F.
  • Herramienta Refleja-en-recta. Reflejamos el punto F en la recta b, obteniendo el punto F'.
  • Herramienta Ángulo. Creamos el ángulo () entre N, E y F. Lo ocultamos.
  • Herramienta Circunferencia. Trazamos la circunferencia con centro F que pasa por B.
  • Herramienta Intersección. Indicamos el punto de corte (G) de la circunferencia anterior con la recta b. (Debemos crear un único punto, señalando con la herramienta el punto de intersección; si señalamos la circunferencia y la recta por separado se crearían dos puntos de intersección.) Ocultamos la circunferencia.
  • Herramienta Ángulo. Creamos el ángulo (β) entre G, F y B. Lo ocultamos.
  • Entrada: H = Rota[B, -z(t-3) β, F]
  • Herramienta Refleja-en-recta. Reflejamos el punto H en la recta b, obteniendo el punto H'. Ocultamos la recta b.
  • Herramienta Segmento. Creamos los segmentos FH y F'H'.
  • Herramienta Arco-centro. Creamos los arcos de centro F desde H a B, y de centro F' desde B' hasta H'.

Añadimos algunos elementos de ayuda visual del procedimiento empleado.

 En algunos momentos, algunos puntos distintos coincidirán en la misma posición. En esos casos resulta especialmente aconsejable seleccionarlos en la Vista Algebraica en vez de en la Vista Gráfica.

Práctica Etapa 4
  • Asignar a t el valor 0.5.
  • Entrada: J = B + z(t) (N - B)
  • Entrada: J' = B' + z(t) (N - B')
  • Herramienta Paralela. Trazamos la paralela a la recta c por el punto D.
  • Asignar a t el valor 1.5.
  • Entrada: K = N + z(t - 1) (E - N)
  • Herramienta Segmento. Creamos el segmento entre N y K. (Asegurarse de elegir N, y no J o J'.)
  • Asignar a t el valor 2.5.
  • Entrada: L = Rota[N, z(t - 2) α, E]
  • Entrada: L' = Rota[N, -z(t - 2) α, E]
  • Herramienta Ángulo. Creamos el ángulo entre N, E y L. (Asegurarse de elegir esos tres puntos exactamente.)
  • Herramienta Ángulo. Creamos el ángulo entre L', E y N. (Asegurarse de elegir esos tres puntos exactamente.)
  • Entrada: {Polígono[N, F, F']}

Introducimos la imagen sobre la que se deberá reproducir la construcción.

Práctica Etapa 5
  • Entrada: Traslada[imagen1, Vector[(10, 0)]]    Asignamos a la imagen 50% de sombreado en sus propiedades.
  • Entrada: B + (10, 0)
  • Entrada: Recta[M + (10, 0), EjeY]

Ocultamos los ejes y mejoramos el estilo de los objetos.

Además, elegimos qué objetos mostramos, e incluso en qué momento. Por ejemplo, decidimos que el triángulo equilátero de la lista1 se visualice sólo a partir del momento en el que el deslizador t alcance el valor 3, simplemente introduciendo en sus propiedades avanzadas la condición t>3 como condición para exponer el objeto.

Ejemplo de construcción
Práctica El arco

 

 

Construcción: El arco

Clic en esta imagen abre la construcción de GeoGebra

 

Práctica Propuesta de construcción

 

 

Realizar una construcción similar con el arco de medio punto, más sencillo, correspondiente a la siguiente imagen:

 

 

Sugerencia: como primer paso, colocar tres puntos sobre el arco, trazar la circunferencia correspondiente usando la herramienta  Circunferencia-3-puntos y situar su centro, de forma que la circunferencia se ajuste lo máximo posible al arco.

 

Comentarios

Las construcciones de este tipo son muy atractivas, pero tienen el inconveniente de exigir bastante tiempo de elaboración. La razón estriba en que no nos limitamos a construir la figura sino que debemos añadir varios elementos auxiliares, con animaciones controladas, para mostrar cada uno de los pasos realizados en su momento preciso.

Investigación Investigación:

  • Existe una amplia variedad de tipos de arcos, así como de otros elementos arquitectónicos, decorativos o informativos (como rosetones, mosaicos, cúpulas, frisos, columnas, logotipos, azulejos, iconos, señales, banderas, cenefas, verjas, escudos, baldosas, máquinas, utensilios, etc.), que podemos usar como modelos sobre los que trabajar. También existen modelos naturales (frutas y frutos, flores, árboles, caparazones y conchas, pieles, cristales, diatomeas, celdas, estrellas de mar...). Algunos modelos se pueden encontrar directamente en la sección Imágenes, pero existen muchísimas otras imágenes en Internet que podemos buscar.

 

Anterior    Arriba     Siguiente