En el modelo Trasvases (en "Otros modelos" del módulo 5) podemos ver una aplicación de este teorema para resolver geométricamente el clásico problema de trasvasar líquidos.

Clic en esta imagen abre la construcción de GeoGebra

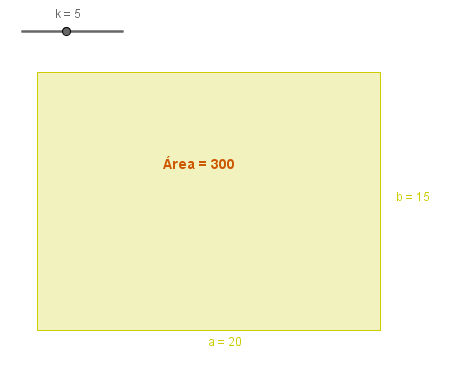
En esta construcción GeoGebra nos ayuda a resolver un problema a la vez que, en el proceso de construcción, nos invita a reflexionar sobre el significado de la proporcionalidad.

Enunciado: "Las medidas de los lados de un rectángulo, en centímetros, son números enteros. La razón del largo al ancho es de 4 a 3. El área es de 300 cm². ¿Cuánto mide cada lado?"

Clic en esta imagen abre la construcción de GeoGebra

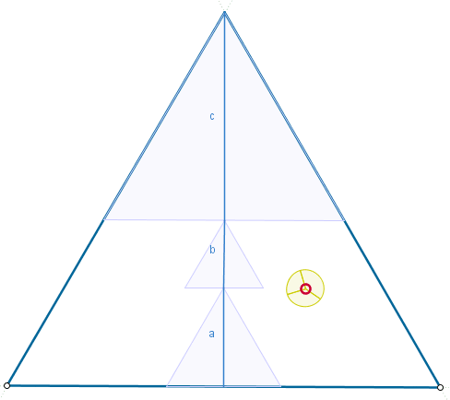
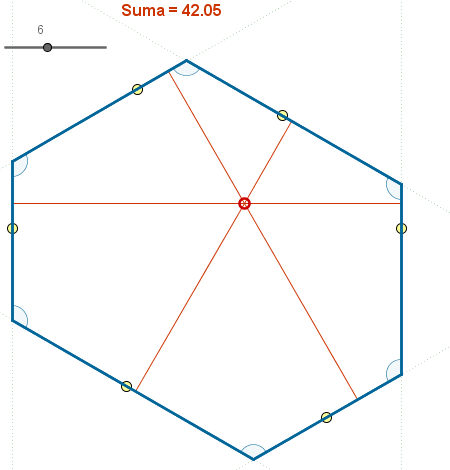
Según el teorema de Viviani, "en todo triángulo equilátero la suma de las tres distancias de un punto interior a los lados es constante". La importancia de la regularidad del triángulo no reside aquí en que sus lados sean iguales, sino en que lo sean sus ángulos interiores. De hecho, esta propiedad es compartida por todos los polígonos equiangulares, sean o no regulares.

Clic en esta imagen abre la construcción de GeoGebra

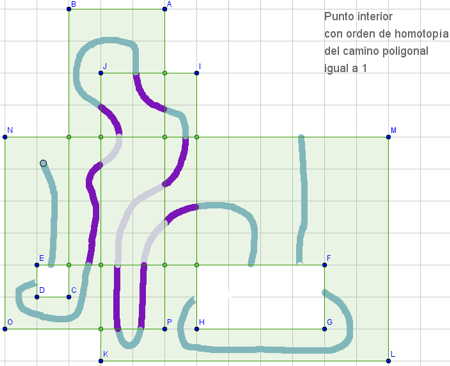
La diferencia entre interior y exterior de un polígono es clara cuando el polígono es simple (es decir, no se interseca a sí mismo). Pero si observamos la parte que GeoGebra sombrea en los polígonos complejos, como el de la figura, nos podemos llevar alguna sorpresa.

El área sombreada en la figura es de 86 unidades cuadradas. Sin embargo, GeoGebra le otorga al polígono un valor de 118. La razón es que hay regiones que el polígono rodea más de una vez (en un sentido o en el sentido opuesto).

GeoGebra suma los ángulos (entre - y ) desde cada punto interior a cada par de vértices consecutivos. Si esa suma es 0, el punto es exterior. Si es distinta de cero, indica (módulo 2) cuántas vueltas da el polígono alrededor del punto, y en qué sentido (positivo o negativo).

El valor que GeoGebra asigna al polígono es la suma del producto de cada área parcial por la suma de ángulos (módulo 2) correspondientes a esa área. En este caso, la suma de 9 por 0 (los "huecos", rodeados por una vuelta en sentido positivo y por otra en sentido negativo) más 62 por 1 (62 u.c. rodeadas por una sola vuelta en sentido positivo, rastro verde) más 16 por 2 (16 u.c. rodeadas por dos vueltas positivas, rastro violeta) más 8 por 3 (8 u.c. rodeadas por 3 vueltas positivas, rastro gris):

polígono = 9·0 + 62·1 + 16·2 + 8·3 = 118

Clic en esta imagen abre la construcción de GeoGebra