Objetivos

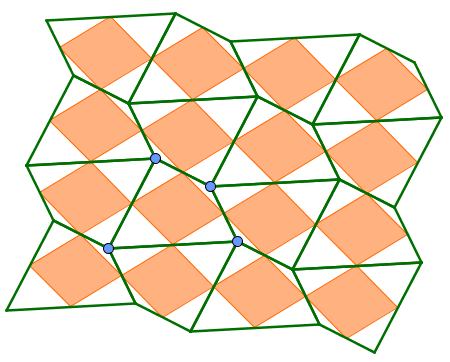
Usaremos GeoGebra para mostrar que cualquier cuadrilátero, convexo o cóncavo, tesela el plano. Para ello, haremos visible la red de paralelogramos que se forma al unir los puntos medios de cada uno (teorema de Varignon).

Del hecho de que cualquier cuadrilátero tesela, se desprende que cualquier triángulo también (basta reflejarlo por un lado para obtener un cuadrilátero).

Herramientas y comandos

Recurriremos a los comandos Polígono, PuntoMedio, Refleja y Segmento. Usaremos además la siguiente herramienta (y una herramienta personal que crearemos para esta construcción).

Punto

Construcción paso a paso

 Antes de empezar, puede ser buena idea echar un vistazo al "Ejemplo de construcción" que se encuentra en esta página. Incluso podemos ayudarnos de la Barra de Navegación para realizar un rápido recorrido por los pasos.

Nos ayudaremos de una herramienta personal. Primero guardamos en un lugar localizable del disco duro la imagen que asignaremos a la nueva herramienta.

Preparación No No Desactiva Guardar la imagen que servirá de icono de la herramienta que vamos a crear en el disco duro (hacer clic derecho sobre la imagen y elegir "Guardar imagen como..."):

Realizaremos el proceso que después guardaremos como herramienta personal.

Etapa 1 Con la herramienta Punto creamos 4 puntos (A, B, C y D). Entrada: C' = Refleja[C, PuntoMedio[A, B]] D' = Refleja[D, PuntoMedio[A, B]] {Segmento[A, B], Segmento[B, D'], Segmento[D', C'], Segmento[C', A]} {Polígono[PuntoMedio[A, B], PuntoMedio[B, D'], PuntoMedio[D', C'], PuntoMedio[C', A]]} Damos un color diferente (y fácilmente diferenciable, como el rojo o el naranja) a esta última lista.

Ahora crearemos la herramienta personal.

Etapa 2 En el menú Herramientas, pulsamos sobre "Creación de Herramienta Nueva". En la primera pestaña, "Objetos de Salida", elegimos mediante la lista desplegable C', D', lista1 y lista2. En la segunda pestaña, "Objetos de Entrada", elegimos los puntos A, B, C y D (en este orden). En la última pestaña, "Nombre e icono", como nombre de herramienta escribimos: ReflejaMedio como ayuda a la herramienta escribimos: Cuatro vértices ordenados y como icono buscamos y seleccionamos la imagen que hemos guardado previamente. Pulsamos el botón Concluido.

Sólo tenemos que usar repetidas veces la herramienta creada (sobre los puntos B,C,D,A, luego sobre C,D,A,B, etc.) para concluir la construcción.

Podemos cambiar el estilo de los objetos desde el cuadro de diálogo Propiedades, eligiendo todos los del mismo tipo (clic en el nombre del tipo) o varios a la vez (Ctrl+clic o Mayús+clic) en el panel izquierdo de ese cuadro.

Ejemplo de construcción

Red invisible

Clic en esta imagen abre la construcción de GeoGebra

Propuesta de construcción

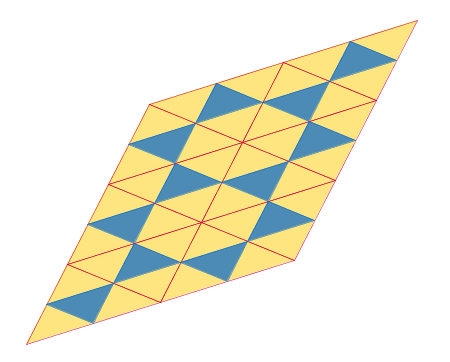
Realizar una construcción similar con triángulos en vez de cuadriláteros:

Comentarios

Gran parte de la matemática se dedica, en última instancia, a la búsqueda de la regularidad. Encontrar patrones ocultos, sean numéricos o geométricos, a veces es sencillo y a veces puede llegar a ser prácticamente inabordable. En cualquier caso, la visualización dinámica de los objetos geométricos, o de modelos geométricos de distribuciones numéricas, puede sernos de gran ayuda.

 Investigación:

• En el caso de los triángulos de la propuesta de construcción, ¿se teselaría el plano reflejando por puntos que no estuviesen justo en el centro de cada lado, sino cuya razón simple con respecto a los extremos del lado fuese distinta a 0.5? ¿O se formarán "huecos" hexagonales?