|
|
► Inicio
► Presentación
Qué es GeoGebra
GeoGebra es un Programa Dinámico para el Aprendizaje y Enseñanza de las Matemáticas que combina elementos de Geometría, Álgebra, Análisis y Estadística. Es muy fácil de aprender a usar y se puede conseguir gratuitamente en su página oficial:
GeoGebra es un programa realizado en Java, lo que garantiza su portabilidad (se puede ejecutar en Windows, MacOS X, Linux o Solaris). Además, basta un par de pulsaciones del ratón para publicar en una página web cualquier construcción que hayamos realizado.
GeoGebra está diseñado con mentalidad colaborativa. Desde la página oficial disponemos de acceso a ayudas, recursos, foros y wikis que usuarios de todo el mundo mantienen en constante renovación.
Geo + Gebra
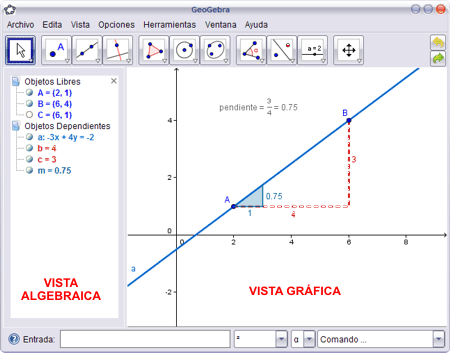
Además de la gratuidad y la facilidad de aprendizaje, la característica más destacable de GeoGebra es la doble percepción de los objetos, ya que cada objeto tiene dos representaciones, una en la Vista Gráfica (Geometría) y otra en la Vista Algebraica (ÁlGebra). De esta forma, se establece una permanente conexión entre los símbolos algebraicos y las gráficas geométricas.
GeoGebra visualiza a la vez un punto en el plano cartesiano y sus coordenadas numéricas, una circunferencia y su ecuación, la gráfica de una función y su expresión simbólica, etc.
GeoGebra es un programa innovador. Posee características propias de los programas de Geometría Dinámica pero también de los programas de Cálculo Simbólico. Incorpora su propia Hoja de Cálculo, un sistema de distribución de los objetos por capas y la posibilidad de animar manual o automáticamente los objetos.
 Formas de usar GeoGebra
Formas de usar GeoGebra
GeoGebra puede servir de ayuda tanto al estudiante como al profesor.
- Herramienta del estudiante: para realizar construcciones desde cero, ya sean dirigidas o abiertas, de resolución o de investigación.
- Herramienta del profesor: para realizar materiales educativos estáticos (imágenes, protocolos de construcción) o dinámicos (demostraciones dinámicas locales, applets en páginas web).
En cualquier caso, sirve de ayuda para que los estudiantes puedan:
- Visualizar conceptos abstractos.
- Representar conexiones conceptuales.
- Experimentar con las matemáticas.
En los tres apartados siguientes podemos ver algunos ejemplos, la mayoría presentados por el propio autor del programa y su mujer, Judith y Markus Hohenwarter.