Reloj solar

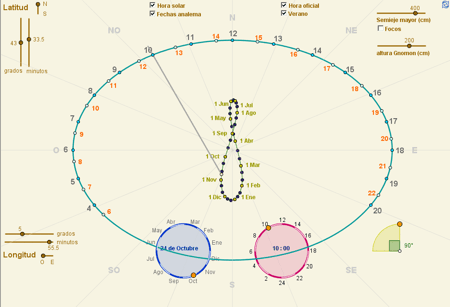
La posibilidad de abatir el plano realza el atractivo de la construcción.

Clic en esta imagen abre la construcción de GeoGebra

 Primos

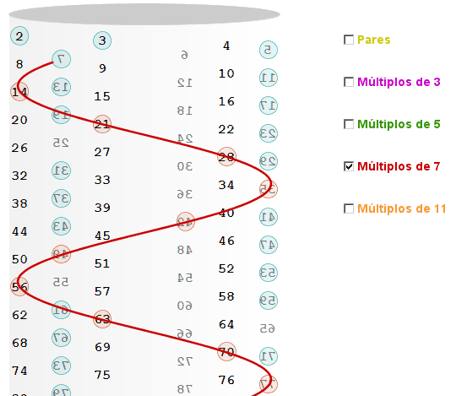
Una versión cilíndrica de la criba de Eratóstenes nos sirve de soporte para observar cómo los múltiplos de cada primo se encuentran sobre hélices cilíndricas si se interpreta el gráfico en tres dimensiones, o sobre sinusoidales si se interpreta en dos.

Clic en esta imagen abre la construcción de GeoGebra

 Dualidad cubo - octaedro

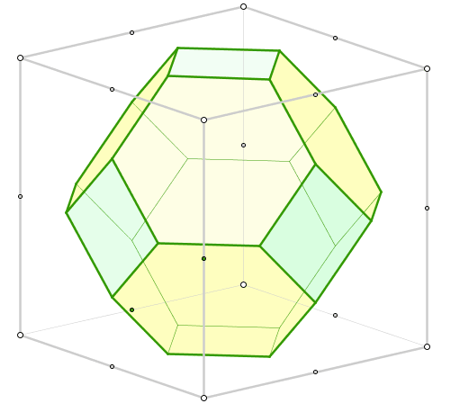
La siguiente construcción se inicia con un cubo y permite la observación de las transformaciones que sufre el poliedro al someterlo a un proceso continuo de truncamiento. Vemos así cómo van apareciendo distintos poliedros irregulares, y algunos semirregulares como el cubo truncado, el cuboctaedro y el sólido de Kelvin (en la imagen), hasta llegar al poliedro regular dual del cubo que es el octaedro, y a partir de este de nuevo hacia el cubo.

Clic en esta imagen abre la construcción de GeoGebra

 Cilindro

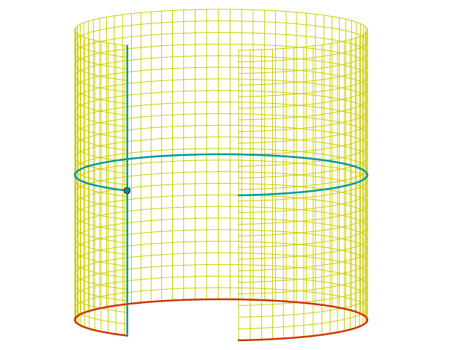
Objetivo: intentar relacionar la expresión paramétrica y gráfica. En este caso mostraremos varios ejemplos, pues se trata de estimular el aprendizaje por comparación y contraste entre expresiones y gráficas.

Ejemplo: (cos(u), sin(u), v)

Clic en esta imagen abre la construcción de GeoGebra

 Cono

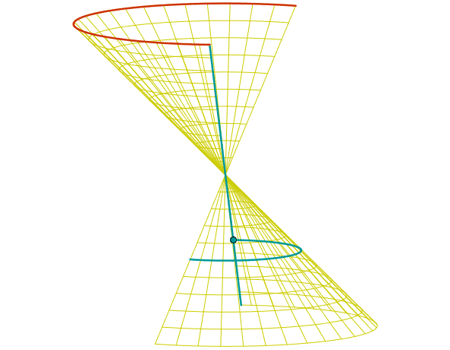
Objetivo: intentar relacionar la expresión paramétrica y gráfica. En este caso mostraremos varios ejemplos, pues se trata de estimular el aprendizaje por comparación y contraste entre expresiones y gráficas.

Ejemplo: (v cos(u), v sin(u), v)

Clic en esta imagen abre la construcción de GeoGebra

 Superficies de revolución

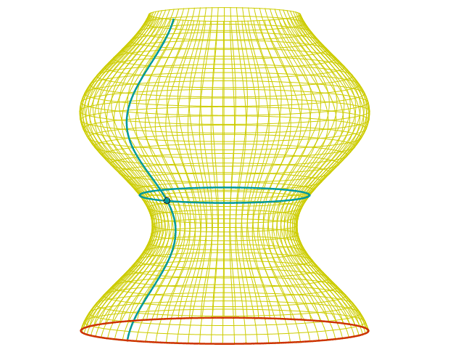
Objetivo: intentar relacionar la expresión paramétrica y gráfica. En este caso mostraremos varios ejemplos, pues se trata de estimular el aprendizaje por comparación y contraste entre expresiones y gráficas.

Ejemplo: (f(v) cos(u), f(v) sin(u), v)

Clic en esta imagen abre la construcción de GeoGebra

 Esfera

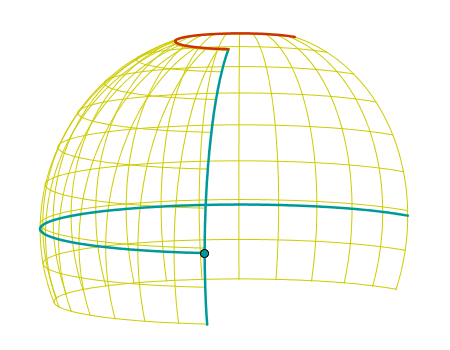
Objetivo: intentar relacionar la expresión paramétrica y gráfica. En este caso mostraremos varios ejemplos, pues se trata de estimular el aprendizaje por comparación y contraste entre expresiones y gráficas.

Ejemplo: (cos(u) sin(v), sin(u) sin(v), cos(v))

Clic en esta imagen abre la construcción de GeoGebra

 Cinta de Möbius

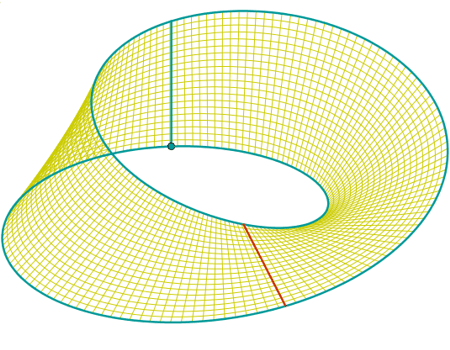
Los modelos virtuales pueden ser un excelente complemento de los realizados con papel.

((1+v cos(u/2)) cos(u), (1+v cos(u/2)) sin(u), v sin(u/2))

Clic en esta imagen abre la construcción de GeoGebra

 Nautilus

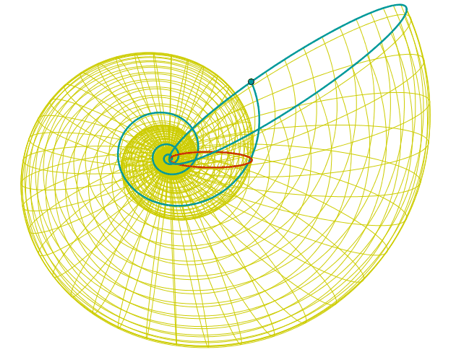
Las curvas paramétricas también se agrupan en familias. Aquí mostramos un representante de la familia de "caracolas", cuya naturaleza se basa en "dar vueltas" (funciones trigonométricas) mientras aumentan su capacidad de crecimiento (funciones exponenciales).

(e^0.2u (1+cos(v)) cos(u), e^0.2u (1+cos(v)) sin(u), 0.6 e^0.2u sin(v))

Clic en esta imagen abre la construcción de GeoGebra

 Curva de Viviani

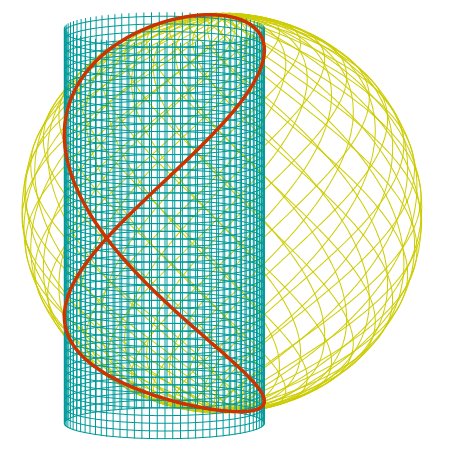
Intersección de esfera y cilindro.

Clic en esta imagen abre la construcción de GeoGebra